Dominion Reinforcement Learning Project

Introduction

The Dominion game box

The aim of this project was to experiment with reinforcement learning. A simplified, single-player version of the card game Dominion was written in Python, and then a reinforcement learning agent was trained to find optimal strategies for the game.

Reinforcement learning is a machine learning approach in which an agent learns to make decisions by performing actions in an environment and observing the rewards obtained. Initially the agent chooses actions by trial and error, but eventually it learns which actions lead to the greatest rewards, allowing it to develop an optimized strategy over time.

Dominion is a deck-building card game in which players begin with identical decks of basic cards, and strategically acquire new action, treasure and victory point cards in order to build increasingly powerful combinations while racing to collect the most victory points by the end of the game. Dominion provides an interesting environment for reinforcement learning because optimal play often requires creating complex combinations of multiple cards, which might be difficult to discover by trial and error alone.

A secondary goal of the project was to experiment with current AI coding capabilities. Claude was used to help write both the Dominion game environment and the reinforcement learning algorithm.

GitHub Link

The project is hosted on GitHub at: https://github.com/sdthompson1/dominion-rl.

Brief explanation of deep Q-learning

Consider an agent playing a game which has a set of possible game states, and a set of actions that the agent can perform. Each action gives the agent a reward (which might be zero, positive or negative), and then either puts the game into a new state or ends the game.

The goal of deep Q-learning is to find a strategy for the game that maximizes the agent's (expected) total reward. This is done by trying to learn a representation for the function "Q(s,a)", which is defined as follows: if the agent is currently in state "s", plays action "a" immediately, and then plays optimal actions until the end of the game, then the agent's expected total reward (from now until the end of the game) is Q(s,a).

(This is actually a slight over-simplification, as usually a "discount factor" is applied, to encourage the agent to prefer rewards obtained soon over rewards obtained in the distant future, but we will gloss over that here.)

Observe that if the Q function is known, then an optimal strategy for the game can be easily determined; given a current state "s", one simply has to inspect the values of Q(s,a) for all possible actions "a", and then pick the action "a" that maximizes Q(s,a).

Of course, in reality, we do not know the Q function. Reinforcement learning (or more specifically, Q-learning) attempts to learn the Q function by experimenting with different actions from different states and seeing what happens.

Since there are a large number of possible game states "s", we cannot hope to make a big table of Q(s,a) values for each possible state-action pair (s,a). Instead, we use approximation. For "deep Q-learning" in particular, we use a deep neural network, in which the input is a vector of numbers representing the game state ("s"), and the output is a vector of numbers, one for each possible action "a", representing the value of Q(s,a) for that particular "a".

The idea is then to play several games, observing the obtained rewards, and adjusting the weights in the neural network to make the approximated Q(s,a) function closer to the actual observed rewards. Eventually, the learned Q function should get reasonably close to the actual Q function, at least for the parts of the state space that the agent actually explored during its runs, and therefore, something approximating an optimal strategy can be discovered.

A key challenge in Q-learning is balancing exploration versus exploitation. "Exploration" means trying new actions to discover potentially better strategies, even if they seem suboptimal based on current knowledge; "exploitation" means selecting the action that appears best according to the current approximation of the Q function. Too much exploitation might trap the agent in a locally optimal but globally suboptimal strategy, while too much exploration wastes time on unpromising actions. Effective Q-learning implementations typically use strategies like epsilon-greedy (choosing the best-known action most of the time, but occasionally, with probability "epsilon", selecting a completely random action), or softmax action selection, to balance these competing priorities during training.

Related Work

This section describes other related work in the area of reinforcement learning for games in general, and Dominion in particular.

The first application of (a form of) reinforcement learning to game playing was apparently Arthur Samuel's checkers player for the IBM 701 in the 1950s. Later work included TD-Gammon (1992) which used temporal difference learning to achieve expert-level backgammon play. Other successes include AlphaGo (for Go, 2016) and AlphaZero (for chess, 2017) although these use other techniques in addition to reinforcement learning.

Reinforcement learning has also been applied to videogames, with the Arcade Learning Environment (ALE), a collection of 57 Atari games, being a popular benchmark in which much progress has been made.

For Dominion specifically, early bots, such as Geronimoo's Dominion simulator (2012) or Matt Fisher's Provincial (2014), used hand-coded strategies; Provincial is apparently regarded as challenging for experienced players. More recent bots are more advanced, e.g. the commercial Dominion app by Temple Gate Games (2021) uses a number of techniques inspired by AlphaZero, as descibed in this blog post.

Other works on AI algorithms for Dominion include Halawi et al (2024), Gerigk and Engels (2023) and references therein, Angelopoulos and Metafas (2021), Fernandez and Anderson (2020). and Ian W. Davis's blog series.

Another interesting line of work, including Ford and Ohata (2022) and Mahlmann et al (2012), looks at using AI to determine well-balanced card sets for the game.

Methods

This section describes the work that was done as part of this project.

Python Code

A Python program for reinforcement learning, along with a corresponding Dominion environment, was created, as follows.

First of all, an abstract Environment interface for a "game environment" was written. This supports the following operations:

A concrete implementation of this interface for a simplified, single-player version of Dominion was then created. In this simplified game, the player starts with a deck of 7 coppers and 3 estates as normal, and then they just have a fixed number of turns (15) to accumulate as many victory points as possible; the normal game ending conditions are ignored. Currently around 20 cards (from the base set, Seaside and Alchemy) are supported. Of these, some are standard cards (such as Copper, Duchy or Curse) which are included in all games; the rest are Kingdom cards, up to 10 of which may be included in any particular game.

The Dominion game logic is mapped on to the Environment interface as follows. First of all, the game state is encoded as a vector of 117 floating point numbers; this includes the counts of all possible card types in each of five possible "zones" (hand, deck, discard pile, in play, "duration" cards, and the supply), together with a few general parameters (such as current coins, actions and buys, current turn number and game phase, etc.). The "actions" that the agent can take include things like buying or playing cards, or skipping the current game phase and moving on to the next one. Finally, the "reward" from an action is simply the number of victory points scored as a direct result of the action. For example, buying a Province would give a reward of 6, while buying a Curse would give a reward of -1. Meanwhile, things like buying Treasure cards or playing Actions would give zero reward initially, but might lead to opportunities for greater rewards later on.

Having discussed the Environment, we now turn to the reinforcement learning algorithm itself. A deep Q-learning system was implemented using the NumPy and PyTorch libraries. This uses a neural network with 2 hidden layers of 64 neurons each (with ReLU activation) to approximate the Q function. The neural network estimates the values of Q(s,a) (for each possible action "a") given a game state vector "s".

The agent uses epsilon-greedy exploration by default. This is good for exploring paths which are close to the current best known strategy, although it is not so good at finding "non-obvious" strategies (complex engines typically fall into this category). The value of epsilon starts relatively high, but it is decreased as training progresses.

The agent is also able to use a form of "imitation learning". This works by playing a fixed, heuristic strategy with probability P, or falling back to the usual epsilon-greedy approach with probability 1 - P. The value of P is slowly reduced as training progresses. This method is useful for finding more complex strategies, e.g. if the fixed strategy is selected to be a complicated engine strategy (which the agent would not be able to discover on its own via trial and error), then the agent is often able to discover an improved version of the engine via the reinforcement learning process.

A simple example of a pre-programmed strategy (using a "Buy Menu", a common method of expressing Dominion strategies) was implemented in the file buy_menu_strategy.py. This was used for some of the experiments described below.

For the learning itself, we use "experience replay" – this means that every time the agent performs an action, a tuple of (state, action, reward, next state, next legal actions) is stored into a replay buffer. Periodically, these tuples are sampled at random and "replayed", which means that the "predicted" reward (as predicted by the current neural network) is compared with the actual reward that was experienced, and the difference is fed to an optimizer as a "loss" value. (Currently we use the "Adam" optimizer with learning rate 1e-3.) The optimizer will then modify the weights in the neural network to try to make the predicted reward closer to the actual reward.

During training, the program periodically stops to evaluate the current strategy. This involves temporarily setting P and epsilon to zero (so that we purely play the best currently known strategy, with no exploration), then playing 500 sample games using the current strategy. The mean and standard deviation of the rewards obtained per game, and various other statistics, are collected.

At the end of training, the program outputs graphs showing the average returns, the distribution of actions selected, and other statistics, as a function of the episode number during training.

Experiments

After some initial testing to verify that the program was working correctly, it was desired to find a set of Kingdom cards for which a relatively complex engine strategy, capable of beating Big Money, was possible, and then to see if the deep learning agent would be able to discover and play that strategy – either on its own, or with the help of the "imitation learning" method described above.

For this purpose, the XML list of strategies from Geronimoo's Dominion simulator was perused, and the "Drunk Marine Students" strategy was selected. This is an interesting and complex strategy involving the University, Wharf, Scrying Pool, Alchemist, Bazaar and Vineyard cards. The reasons for choosing this particular strategy (as opposed to others from that list) were that (a) these cards were relatively simple to implement in the Python code, and (b) the strategy does not rely on Attacks for its success (apart from the minor Attack aspect of Scrying Pool, which can be safely ignored), and therefore is suitable for testing in a single-player environment.

Therefore, in order to see if the bot could reproduce this strategy (or a similar one), a Dominion environment including the following cards was set up:

Cards used for the experiment

This includes all of the standard Treasure and Victory cards as well as the specific cards needed for that strategy. A "Curse" pile was also included, just to see whether the agent would learn to avoid buying Curses.

Having settled on that particular set of cards, a first experiment was run, in which the agent attempted to learn a strategy from scratch (i.e. without using "imitation learning"). The results are described in full below, but the summary is that the agent learned to play a "Big Money + Wharf" type strategy, scoring around 30 points over the 15 turns.

A second experiment was therefore run, in which a predefined Buy Menu strategy, approximating the "Drunk Marine Students" strategy (or some version of it), was set up, and used with the "imitation learning" procedure described above. In this case the agent was more successful, first learning to copy the provided strategy, and then making substantial improvements to it, ending up with a strategy scoring around 40–60 points (albeit with high variance).

We now give the full details of the experimental setup for each of the two runs, before going on to give the results in more detail below.

Experiment 1

Standard Cards used (with initial Supply counts): Copper (60), Silver (40), Gold (30), Potion (16), Curse (20), Estate (12), Duchy (12), Province (12)

Kingdom Cards used (each initially with 10 in the Supply): Alchemist, Bazaar, Scrying Pool, University, Vineyard, Wharf

(Note: The Scrying Pool card is slightly simplified compared to the real game: the Attack element is removed, and the initial revealed card is always put back if it is an Action or discarded otherwise.)

Neural network configuration: Input width 117 (corresponding to the state space size), two fully connected layers of width 64, and output width 19 (one output per card in the game and another one output for the "skip phase" action). All layers use ReLU activation and are initialized using He initialization (also known as Kaiming initialization).

Number of turns in game: 15

Parameters: Learning rate = 1e-3; Discount factor = 0.9999; Epsilon = 0.25 initially, with min 0.001 and decay factor 0.9996; Predefined strategy = Disabled; Batch size = 64; Replay buffer size = 10000; Target update frequency = 1000; Number of episodes = 20000; Sample frequency = 500. (See the Python code to find out precisely what these parameters actually do!)

Experiment 2

Standard and Kingdom cards used, Neural network setup, and Number of turns in game: Same as above

Parameters: Same as above, except: Epsilon decay factor = 0.9999 (instead of 0.9996); Number of episodes = 60000 (instead of 20000); Predefined strategy enabled (see strategy details below), with initial probability = 1.0 and decay factor = 0.9993.

Fixed strategy: For buying and gaining decisions, we use a "buy menu" heuristic. The agent chooses the first entry from the list below which it is actually possible to buy or gain (i.e. the agent has enough money, the supply hasn't run out, etc.).

Note: The "max" numbers mean that this item will be skipped over if the agent already has that many cards (or more) in its possession. For example, the first "Bazaar" entry will be skipped/ignored if the agent already has 3 or more Bazaars; so the agent would prefer a Bazaar over a Vineyard if it has 3 or fewer Bazaars currently, but if it has four or more Bazaars then it would be the other way around.

It should be noted that no particular effort was spend on optimizing this fixed strategy, and indeed it does not do particularly well on its own (it only scores around 10 points), but it does contain the germ of an idea, which the agent is able to develop into something much more powerful after a few thousand episodes of training.

Results

Experiment 1 (standard learning: "Big Money + Wharf")

The learning graphs for Experiment 1 are shown below.

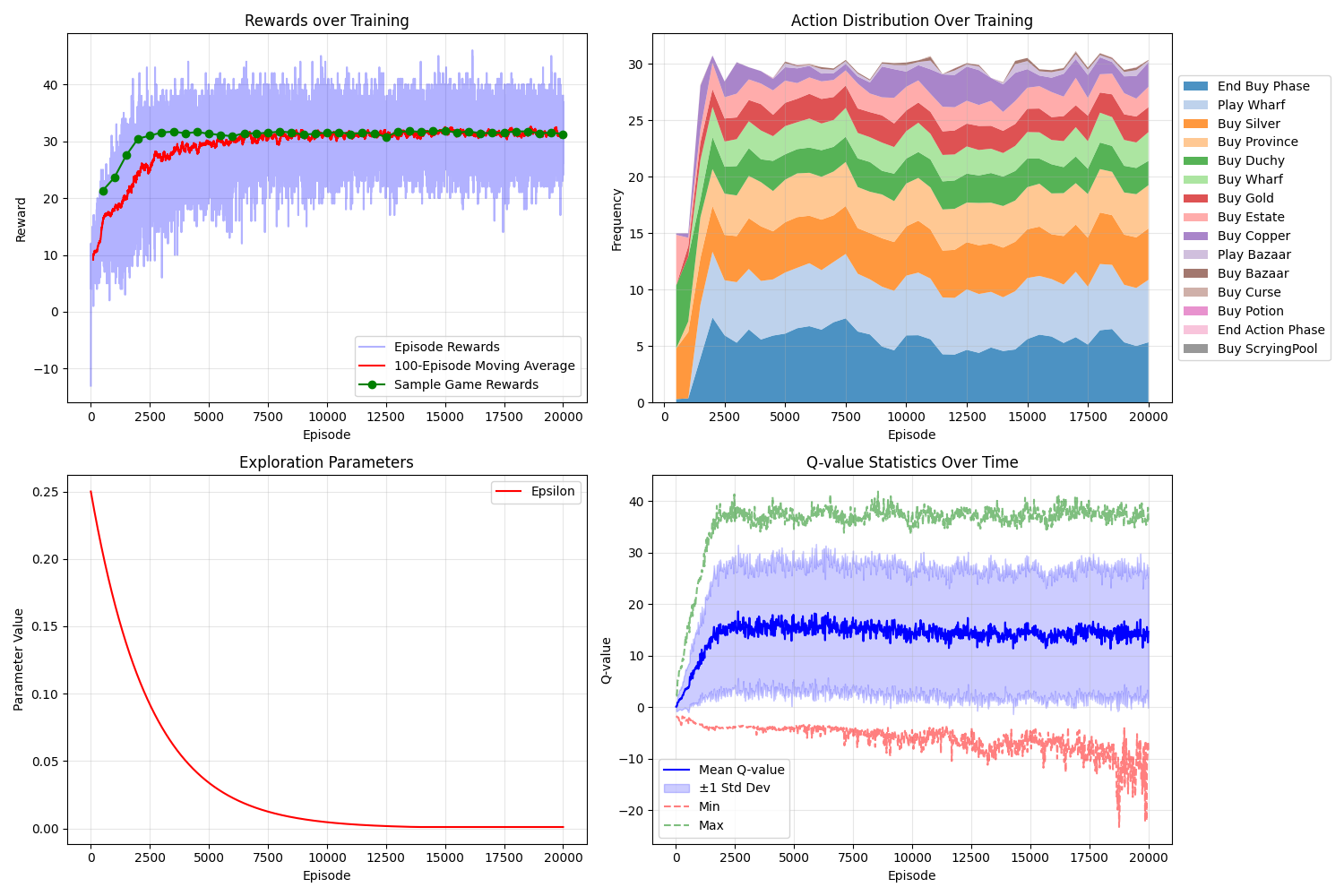
Learning graph for Experiment 1

We see (from the top right graph) that very early in training, the agent is mostly buying Silver, Duchies and Estates. At this point, it has learnt that buying Estates gives you points, and buying Silver allows you to get higher-scoring cards such as Duchies, but it has not yet discovered the Gold or Province cards (at least not to a significant extent).

Later on in the training, the rewards (top left graph) appear to converge, indicating that the agent has successfully learned a reasonable strategy, scoring about 30 points, for this Kingdom set. The dominant actions (top right graph) are:

There is also a small amount of Bazaar usage, but evidently this is not a large part of the strategy.

The agent also does sometimes buy Coppers and Estates, which is perhaps surprising, but maybe it makes sense – one could imagine that buying Estates (when you can't afford anything else) near the end of the game might be useful, and one can also imagine that buying Copper might be helpful in certain situations (e.g. perhaps early in the game to help get the strategy going a bit faster?). (As an aside, it might be useful to extend the program to print out full game logs, so that we could determine at which point – early or late game – the agent is buying the Coppers.)

The final strategy scores just over 30 points on average, with a certain amount of variance (indicated by the light blue shaded area on the top left graph), which is (presumably) a consequence of the randomness introduced by deck shuffling.

Note that the red line in the top left graph shows the rewards obtained during training (while the epsilon-greedy exploration is active), while the green line shows the results of evaluating the best currently known strategy (without any exploration). As expected, the two lines converge as epsilon becomes close to zero (see also lower left plot).

The lower-right plot shows the actual Q-function values recorded during training. It is not clear why the "Min" Q-value becomes slightly "unstable" towards the end, but this does not appear to have caused any adverse effects, as the rewards obtained remain stable.

Experiment 2 (imitation learning: engine strategy)

The graphs for Experiment 2 are presented below. (Recall that this was the case where the agent initially plays a pre-defined Buy Menu strategy before transitioning to normal epsilon-greedy exploration later on.)

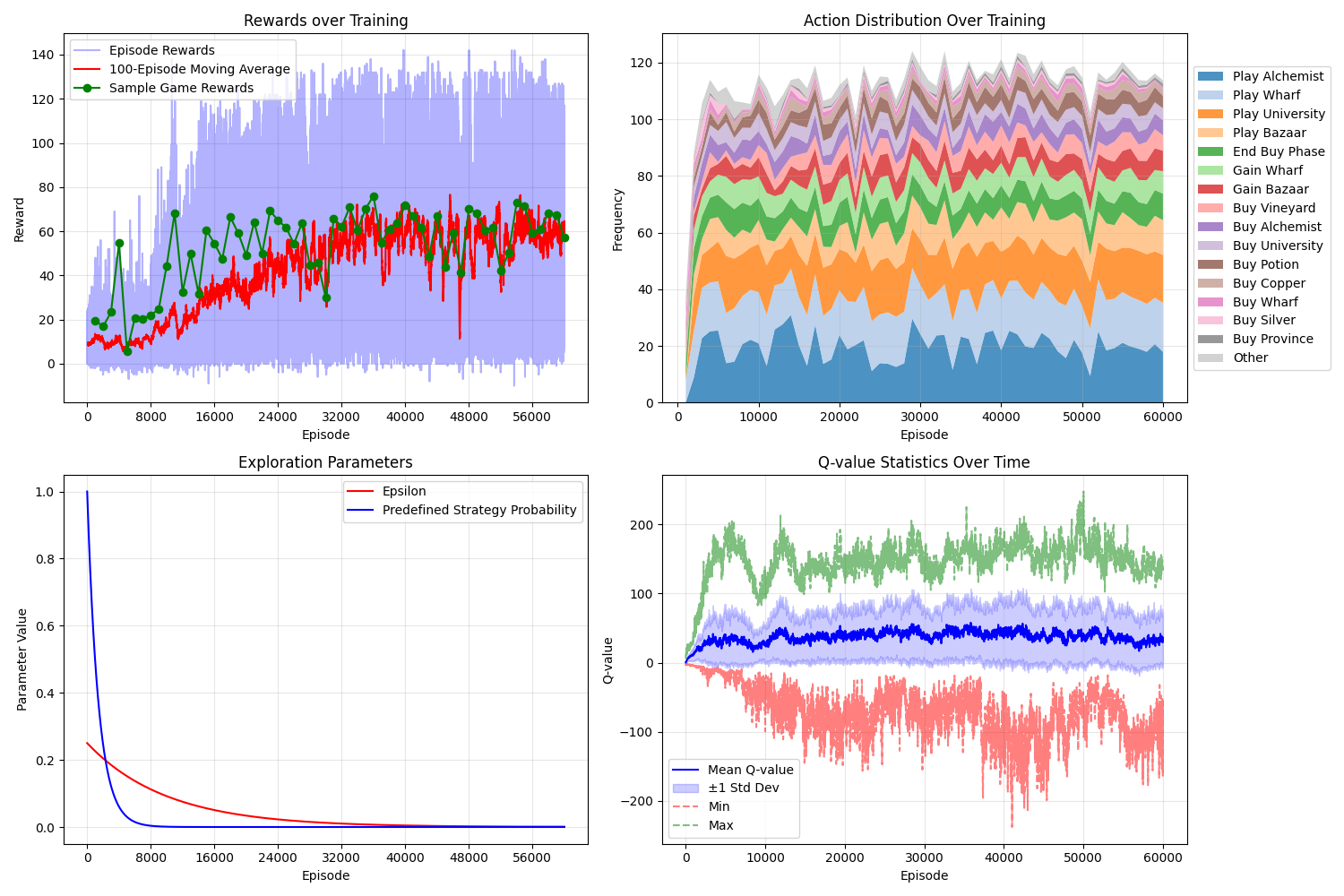
Learning graph for Experiment 2

This shows that agent initially plays a relatively ineffective strategy (based on the pre-defined Buy Menu strategy) for about 20 points, but fairly soon it learns a better strategy scoring around 40–70 points on average.

The average rewards obtained (red and green lines on top left graph) oscillate a lot more than previously, and the per-episode rewards (the light blue background line on the top-left graph) are also highly variable, showing that the bot has apparently learned a highly "volatile" strategy that can in some games score upwards of 120 points, but in other games scores almost zero. The reason for the volatility is not clear: it might be because the bot hasn't learned to play the action cards correctly in all circumstances (meaning that it occasionally "fails" to play its hands correctly, giving it a very low score in those particular games), or it might be because a complex engine strategy is inherently variable (e.g. if you get your +Actions and +Cards in the right order, you can do very well, but e.g. if you get all the +Cards together in one hand with no +Actions then you are a bit stuck). It might also be a combination of those two factors. (Again, studying detailed game logs might shed a bit more light on this.)

The top right graph shows that the strategy involves buying and using multiple Action cards, including Alchemist, Wharf, University and Bazaar. The agent also makes good use of University's ability to gain an Action card costing up to 5 to get more Wharves and Bazaars (both costing 5). Finally, the agent buys Vineyards (which give victory points in proportion to the number of Action cards in the deck), which goes well with the Action-buying strategy.

Note that the strategy does not involve much use of Scrying Pool, which is interesting since the original "Drunk Marine Students" idea from Geronimoo's simulator did include this card. This could be because the strategy really is better off without that card, or it could be because the bot has failed to learn to use that card properly for some reason. (It might also be that the Attack aspect, which was ignored in our experiment, is important and contributes a lot to the win rate in multi-player games; if true, this would explain why the card is not so useful in a single-player environment.)

Note that the strategy found only really works when the cards involved are combined together; buying one or two of the cards on their own, without the others, would likely not score very well. This probably explains why the epsilon-greedy agent was unable to find this strategy. For example, an epsilon-greedy agent might quickly discover a "Big Money" like strategy, but then try to improve it by adding Vineyards. This would not work, because the Vineyards do not score very much on their own. Alternatively, the agent might try to add, say, University to the strategy, but one of the strengths of University is that it allows you to gain a lot of cheap Action cards (thus benefitting your Vineyards); so University without Vineyard probably will not score very well. It is only by combining the two cards (and additionally, learning to use the "gain" ability of University profitably) that you can reach the highest scores; but the epsilon-greedy agent is unlikely to try that, because the probability of it exploring that particular combination of actions by random chance alone is very low. However, starting from the predefined buy menu strategy does work, because the buy menu is already buying a good combination of actions and Vineyards, and there is a continuous "path" from that initial strategy to a much more well-balanced and high-scoring version of the same idea.

Conclusions

The main conclusion from this work appears to be that reinforcement learning is able to learn reasonable Dominion strategies, such as augmented Big Money strategies, on its own, but more complex strategies, such as complex card drawing engines, require human assistance. This could be seen clearly in our two experiments, where the unassisted agent was able to discover Big Money, and was also able to discover that using Wharf together with Big Money is better than Big Money alone, but it was only when domain knowledge (in the form of a predefined Buy Menu) was provided that the agent could discover more complex strategies.

The good news is that one does not need to know the perfect strategy in advance; it seems that providing only a simplified, low-scoring version of an engine is enough, and then the agent is able to refine it into a much higher-scoring version via the reinforcement learning process.

Note that the inability to discover complex, multi-step strategies without human assistance (or more advanced algorithms) seems to be a fundamental limitation of reinforcement learning. For example, we can compare our situation with the Atari games benchmark (see "Previous Work" section above). Early approaches were able to master simple games like Space Invaders, but struggled to score any points at all in more complex games like Montezuma's Revenge or Pitfall, where considerable exploration is required before any rewards can be found. Later approaches, such as Go-Explore or Agent 57, addressed this by using much more sophisticated exploration methods, allowing the agent to discover complex multi-step strategies on its own. Perhaps similar methods could be applied to Dominion to help the agent find those complex engines which the current method (which really just amounts to a form of trial and error) is not able to discover by itself.

Another interesting result was that the strategy found in Experiment 2 appears to have considerable variance in the number of points scored; sometimes it gets over 100 points, and other times almost no points. It is unclear whether this is a learning issue (i.e. some kind of defect in the found strategy), or whether it is inherent to the randomness of these engine-type strategies. Without doing a more detailed analysis of the agent's play patterns, it is difficult to tell; this might be an interesting subject for future work.

Finally, it was mentioned at the beginning that a secondary goal of the project was to experiment with current AI technology (and Claude in particular) to see how much it was able to help with a project like this. I am pleased to say that the AI was very useful – with the assistance of AI, this project was completed in about 2–3 weeks in total, but I think it would have taken longer (maybe twice as long) without AI help. The AI was most effective in helping with the coding; for example, it very quickly wrote an initial version of both the Dominion environment itself, and the reinforcement learning algorithms. It is true that the AI sometimes introduced bugs, and it didn't always structure the code in the best possible way (e.g. the idea to introduce the Environment base class, therefore decoupling the learning agent from the specific environment it was being used with, was done by me), but the AI was still very helpful in quickly writing a "starting point" for the code, which I was then able to improve upon by hand. So I would say that AI is not yet ready to write entire applications completely on its own, but as a tool for increasing the productivity of human programmers, it is very useful. Furthermore, the AI not only helped with writing the code, but it was also useful for other tasks, such as helping to write the README for the GitHub repository, reviewing this document and suggesting improvements, creating a small piece of CSS for this web page, and helping me to use GIMP to lay out the "Dominion cards" image above.

Future work

Aside from simply extending the Dominion environment itself, by introducing new cards or expansions, there are several interesting ways in which this work could be improved or taken in new directions.

First of all, it would be nice to implement logs or visualizations in order to increase the interpretability of the results. For example, full text logs of sample games could be produced, allowing us to directly inspect what the strategies are doing in various situations. Alternatively, perhaps graphs could be created, showing how the cards purchased, actions played, and points scored evolve during the 15 turns of gameplay (either for one particular run, or averaged over many runs). These features would help us better understand what the bot is actually doing, e.g. is it playing the Action cards optimally, or could the strategy be further improved by an expert human player?

Regarding interpretability, another idea is to try to distill the neural network down to a limited number of heuristic rules (e.g. buy X, Y and Z in the early game; switch to buying A, B and C later on; always play action P before action Q; things like that). If a way of doing this successfully could be found, then that could potentially be useful for finding strategies that could be used by human players in real Dominion games, rather than simply programming an AI to play the game.

Moving on, another interesting question is whether it would be possible to train a bot to play on a previously unseen Kingdom set. The method described above works by fixing a Kingdom set and then training the agent to find a strategy for that particular set, but of course, the knowledge gained would not be usable with a different Kingdom. One idea that might work here is to use "transfer learning", e.g. find a strategy that works well on one Kingdom, and then use that strategy as a starting point for another, similar Kingdom. (Or perhaps one could start with a simpler Kingdom and then transfer the knowledge gained to a more complex Kingdom.) Another, different approach could be to try out the "embedding" idea discussed in the Temple Gate Games blog post.

Another major area for future work is to figure out how to get the agent to discover complex engine strategies without the need for human assistance. As mentioned above, the lesson from the Atari work seems to be that more sophisticated exploration strategies are the key to solving this problem. To that end, perhaps something similar to the Go-Explore or Agent 57 algorithms could be tried, or perhaps other techniques, such as intrinsic motivation (curiosity-driven exploration) or random network distillation (RND) could be experimented with. There might also be Dominion-specific approaches that could be tried; for example, one idea is to generate a large number of Buy Menu strategies at random, pick out the higher-scoring ones, and use those as a starting point for exploration and see what happens.

Extending the bot to play multiplayer Dominion would also be interesting. This of course comes with its own challenges, and new techniques, such as self-play or population based approaches, would have to be introduced. It might also be fun to try out any resulting strategies against other real-world Dominion bots, such as Provincial, or indeed against human players.

Finally, another interesting area could be to look at the volatility of the obtained strategies. For example, a strategy that consistently scores 40 points might be preferred over a strategy that sometimes gets 100 points but sometimes gets zero. To this end, techniques such as mean-variance optimization (i.e. both maximizing the mean points scored by the strategy, and minimizing the variance of the score, at the same time) might be considered.

Stephen Thompson
Email: stephen (at) solarflare.org.uk
Last updated March 2025